基于关系思维的语音识别的深度图随机过程
作者:Hengguan Huang^1^, Fuzhao Xue^1^, Hao Wang^2^, Ye Wang^1^
单位:^1^新加坡国立大学;^2^麻省理工学院
发表:ICML 2020
一、简介与思路
关系思维
- 关系思维 relational thinking:在学习的过程中,我们会接收到各种各样的信息,不管是来自视觉、听觉、触觉等,但是我们并不会有意识地去保存它们。在各种各样的信息之间隐藏着联系,这些信息及它们之间的联系组成了我们的percepts(感知)。
- 与关系推断 Relational Reasoning的主要区别:relational reasoning 是有意识地处理这些 relation information。
语音识别任务
人类对话本质上是两个或更多说话者之间交换思想的过程
机器学习中语音识别任务一般被分解为声学建模和语言解码两部分,而忽略了本质上的关系思维过程
关系思维中涉及的感知(例如,在听到声音时形成的心理印象)被认为是无数的,并且不能直接观察到
明确地建模关系思维形成的感知仍然是一个挑战
- 混合声学递归神经网络隐马尔可夫模型(RNN-HMM模型)在许多方面仍然优于用于声学建模的端到端编码器-解码器方法
- RNNs在捕捉顺序输入的长期时间依赖性方面做得很好,但在表示复杂关系方面做得很差
提出一种贝叶斯非参数深度学习方法,深度图随机过程(DGP)
将关系思维中涉及的感知建模为概率图,而在训练过程中不使用任何关系数据
- 感知被建模为当前话语与其历史之间的关系
- 由于知觉的无意识,我们假设这种关系存在的概率接近于零(类似于先验知识)
给定一个话语和它的历史,我们生成无限个由包含在DGP中的概率图表示的感知,其中每个节点描述一个话语的表示,每个边对应于两个节点之间的关系
假设感知图的边是按照伯努利分布分布的,边存在的概率接近于零
从直觉上来理解,在我们接收信息时,信息之间并没有生成稳定的信息,各个信息之间都是会产生关联的,并且基于我们的先验知识和历史信息,会在脑海中产生各种各样的理解 — 相当于接收到的信息的不同组合,而这个组合是有无限可能的。并且,由于这些percepts是无意识的,percept graph中边的概率是接近于0的。
- 通过简单地对邻接矩阵求和来组合无数的图在计算上是很难的(计算与优化方面)
- 创建一个等价的图来找到一个解析解,其中边由二项式变量表示
- 进一步通过一个具有有界近似误差的高斯分布为该二项式分布的推断和采样找到一个近似形式的解
- 为了将新图形转换为“有意识的”或特定任务的图形,我们使用另一个高斯变量对新图形的每条边进行加权,该高斯变量以从二项式变量得出的边为条件
- 计算变换后的图上的图形嵌入,并将其用作声学建模的附加输入
- 为了联合优化上述组件,我们采用了变分推理框架,并成功地导出了一个有效的证据下界
- 创建一个等价的图来找到一个解析解,其中边由二项式变量表示
二、相关工作
1. 图的贝叶斯深度学习
关系堆叠去噪自动编码器(relational stacked denoising auto-encoders, RSDAE):将图结构结合到概率自动编码器中的原则模型,显著改善了表示学习;
关系深度学习(relational deep learning, RDL):有监督和完全贝叶斯版本的RSDAE,以直接处理链接预测任务;
图形自动编码器(graph auto-encoders, GAEs):以无监督的训练方式学习真实世界的图形数据,使用图卷积网络(GCN)编码器使用低维向量表示节点,并使用解码器重建邻接矩阵;
- (↑这些方法应用在:发现化学分子、建模引用网络、构建知识图)
正则图变分自动编码器(Regularized Graph Variational Autoencoders, RGVAE):使用对立的正则化框架来正则化解码器的输出分布,从而改进GAEs;
(Bojchevski et al., 2018)使用随机游走进一步拓展了RGVAE;
- 缺点:以上都是静态图,限制了它们在处理动态图的现实世界问题中的模型泛化能力;
- 变分图循环网络(Variational graph RNN, VGRNN):通过结合GCN,RNN和GAEs来缓解这个问题,允许捕捉动态图的演变;
- 缺点:它们需要图注释(话语之间的关系标注,很多任务都没有关系标注)
2. 变分声学建模
- RNN-HMM声学模型(作为一种HMM分类器)
- 使用RNNHMM对语音信号建模时,会遇到许多不确定性:如背景噪声对语音信号的影响
- 缺点:RNN-HMM在处理这种不确定性方面是有限的,因为RNN本质上是一个确定性函数
变分的RNN(variational RNN, VRNN):引入了一个潜在变量$\bold{z}_{i,t}$,以捕捉时间t时声学特征的不确定性
假设这样一个潜在变量具有高斯先验分布$p\left(\mathbf{z}{i, t} \mid \mathbf{h}{i, t-1}\right)$,该分布依赖于先前的RNN隐藏状态$\mathbf{h}_{i, t-1}$
它的后验分布由变分分布$q\left(\mathbf{z}{i, t} \mid \mathbf{x}{i, t}, \mathbf{h}_{i, t-1}\right)$近似,允许使用证据下界(ELBO)进行联合学习和推理:
后验分布的采样是通过使用基于重新参数化的蒙特卡罗(MC)估计来实现的
可以通过随机梯度下降来训练该模型
- 缺点:VRNN-HMM声学模型的一个主要限制是:所学习的潜在分布表现出不可解释的表示,因为近似分布被假设为采取缺乏表达能力的一般形式
三、关系思维建模
1. 问题定义
序列分类问题。
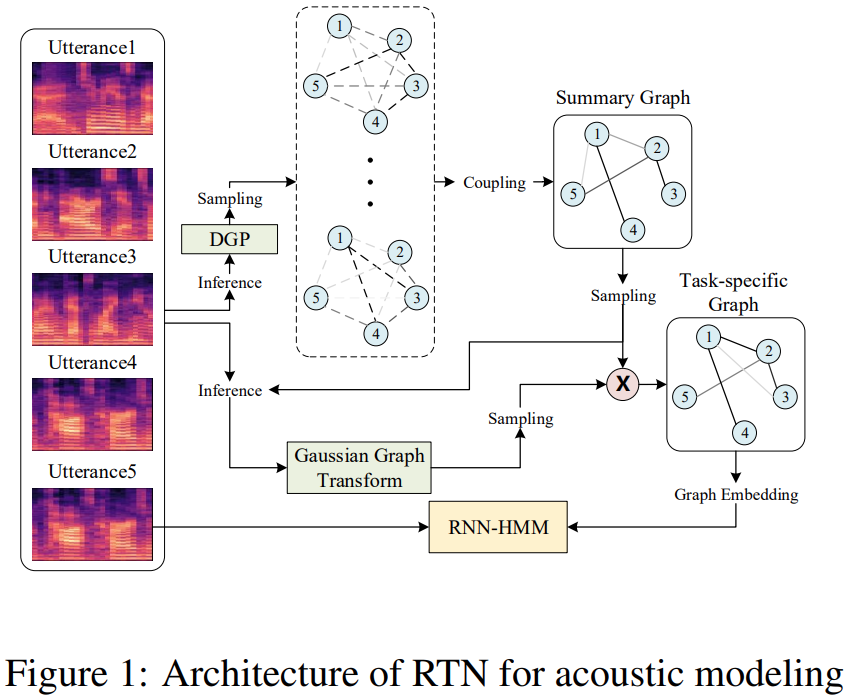
2. 深度图随机过程(Deep Graph Random Process,DGP)
在声学建模中,每个节点代表一个话语,其嵌入是通过对第i个话语的声学特征序列进行编码的神经网络$f_{\theta}$来计算的:
DGP的核心是一系列作为构建模块的深度伯努利过程(DBP),每个过程负责在DGP的两个节点之间生成边
Bern()是伯努利分布,DGP由此生成无数概率图:
(1) 无数概率图的耦合(汇总图的生成)
耦合的目标是获得无限个感知的汇总(summary)。直接进行求和是复杂的。
构建一个等价图,它可以作为原始无数图的总结或表示。它保留原始节点集,并通过从二项分布中采样来更新每个边:
其中$n \rightarrow+\infty$ 、$\lambda_{i, j} \rightarrow 0$。
单个percepet graph中边是服从Bernuli分布的,单考虑一条边的话,summary graph中对应边就是重复的Bernuli抽样,所以可以把summary graph中的边看作是服从Binomial分布的
(2) 汇总图(summary graph) 边的推断和采样
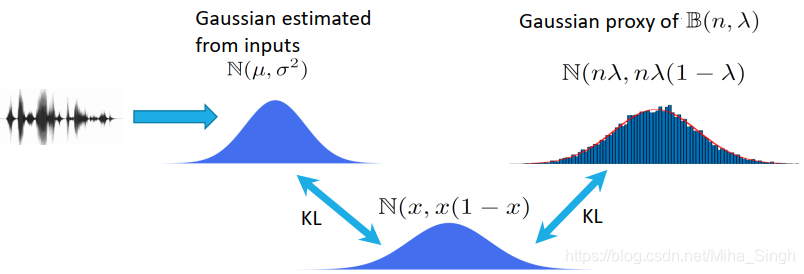
二项分布,且$n \rightarrow+\infty$ 、$\lambda_{i, j} \rightarrow 0$,是难以求解的,采用一个高斯分布来近似上文提到的二项分布。
假设边$(i,j)$服从二项分布$\mathcal{B}\left(n, \lambda{i, j}\right)$,$n \rightarrow+\infty$ 、$\lambda{i, j} \rightarrow 0$。
从VRNN中得到启发,近似后验参数从RNN编码声学特征中估计的。但DGP包含近似后验$q\left(\tilde{\alpha}{i, j} \mid \mathbf{X}{i-o: i}\right)$,由于$n \rightarrow+\infty$,无法简易地进行推理、求解。
理论1:
设$\mathcal{N}\left(\mu, \sigma^{2}\right)$表示$\mu<1/2$的高斯分布,$\mathcal{B}\left(n, \lambda{i, j}\right)$表示$n \rightarrow+\infty$ 、$\lambda{i, j} \rightarrow 0$的二项分布。$n$递增,$\lambda$递减。
存在一个常数$m$,如果$m=n\lambda$,定义:得到:$f_1(x)$在$(0,1)$上达到最小值,$f_2(x)-f_2^*$在$(0, \sqrt{2} / 2- 1/2)$上有界,其中:
假设我们给定一个高斯分布$\mathcal{N}\left(\tilde{\mu}{i, j}, \tilde{\sigma}{i, j}^{2}\right)$,其参数$\tilde{\mu}{i, j}$由神经网络具体参数化,可以保证$\tilde{\mu}{i, j}<1 / 2$(激活函数)。
通过德·莫伊弗-拉普拉斯定理,可知$\mathcal{N}\left(n \lambda{i, j}, n \lambda{i, j}\left(1-\lambda{i, j}\right)\right)$是$\mathcal{B}\left(n, \lambda{i, j}\right)$的很好的近似。当n增加时,它们是渐近等价的。
设$m{i,j}=n\lambda{i,j}$,利用定理1,可以避免无限参数$n$和近零参数$λ{i,j}$的直接参数化,同时它允许使用 (Kingma & Welling, 2013) 的重新参数化技巧。这个技巧**通过高斯代理从二项分布中抽取样本$\mathcal{N}\left(m{i, j}, m{i, j}\left(1-m{i, j}\right)\right)$,$m{i,j}=n\lambda{i,j}$(每条边的近似高斯分布)**。
3. 将DGP应用于声学建模
- 高斯图变换
关系思维的另一个重要方面是,它将无数无意识的感知转化为可识别的知识概念;目标是从代表我们下游任务的无数感知图的摘要图中提取一个信息表示—声学建模;通过用高斯变量$s_{i,j}$对每个边进行加权来转换概要图来实现的:(很像注意力机制)
进一步假设这样的高斯变量被限制在summary图的边$\tilde{\alpha}{i, j}$上,以避免在边$\tilde{\alpha}{i, j}$的一些值接近零时,这样的高斯变量的分布(如果它独立于边$\tilde{\alpha}_{i, j}$)随机地表现。其定义为:(假设:权重是以summary graph边的取值为条件的)
这种操作为高斯图变换。生成的图形称为特定任务的图(task-specific graph)。
得到task-specific graph后,即可按照GNN/GCN的方式获得graph embedding(注意:每处理一个utterance时都会有对应的task-specific graph)。
- 图嵌入
然后,从节点$\bold{v}_i$对应于当前话语的变换图中提取图嵌入$\bold{e}_i$:
其中$f_θ$是神经网络,$\bar{E}$是变换图的边集。
- 整体模型
生成的图形嵌入$\bold{e}_i$作为我们的声学模型的附加输入
整个框架称为关系思维网络(RTN),使用简单循环单元SRU作为基本构件
SRU简化了LSTM的体系结构,显著提高了计算速度,而几乎没有降低性能
RTN的更新公式:(将graph embedding与原来的输入进行拼接,作为输入)
$\mathbf{r}{i, t}$是重置门的输出,$\mathbf{f}{i, t}$是遗忘门的输出,$\mathbf{c}_{i, t}$是记忆单元输出,$σ$是sigmoid激活函数。
4. Learning:训练&优化
采用变分推理来联合优化DGP、高斯图变换和声学模型
DGP可以等效地表示为两种类型的随机变量:与感知图的边相关的伯努利变量和与summary图的边相关的二项式变量
虽然这两个随机变量在概率分布上有不同的形式,但我们可以用这两个不同的随机变量来描述相同的随机过程数据
指定DGP的二项式变量完全决定了整个图随机过程。最终目标是最大化证据下界(ELBO):
其中,$\tilde{\mathbf{A}}=[\tilde{a}{i,j}]$是汇总图的邻接矩阵;$\mathbf{S}=\left[\tilde{s}{i, j}\right]$是高斯图变换矩阵;$p\left(\tilde{\mathbf{A}}, \mathbf{S} \mid \mathbf{X}{i-o: i}\right)$是$\tilde{\mathbf{A}}$和$\mathbf{S}$上的联合先验分布,$q\left(\tilde{\mathbf{A}}, \mathbf{S} \mid \mathbf{X}{i-o: i}\right)$是相应的近似后验分布
由于S的每个元素都受汇总图同一边的二项式变量的制约,KL项可以进一步写成:
由于$n \rightarrow+\infty$,第一项KL在计算上很难处理,要对其进行转化
理论2
给定两个二项分布$\mathcal{B}\left(n, \lambda\right)$、$\mathcal{B}\left(n, \lambda^{0}\right)$,其中$n$是增加的,而$λ$和$λ_0$是减少的
存在一个实常数$m$和另一个实常数$m^{(0)}$,如果$m = nλ$和$m^{(0)}= nλ^{(0)}$,并且如果$λ > λ^{(0)}$,有:
根据定理2,可以得到一个与n无关的封闭形式的解
四、实验及分析
使用当前语句与历史9句话来构建图
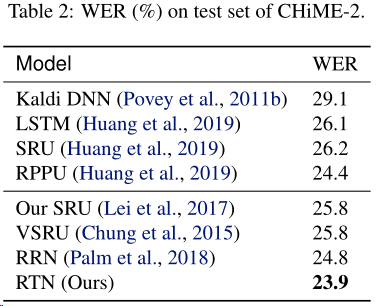
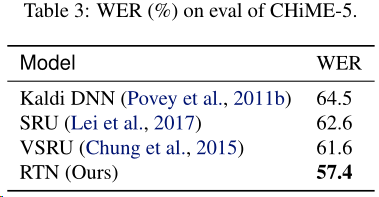
CHiME-2、CHiME-5数据集
RelationalSWB数据集
DGP关系的定量评价
在RelationalSWB数据集评估了图的边与基本事实关系的匹配程度
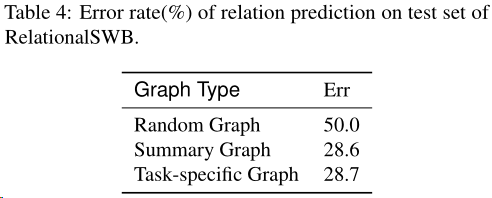
在RelationalSWB数据集的实验结果:
DGP对SWB和SwDA的定性评价
- 右边显示的总结图比左边的连接更密集
- 能够捕获话语之间的强弱关系

五、结论
提出了一种新的图学习方法,称为深度图随机过程(DGP),用于关系思维建模
模型可以生成表示话语之间复杂关系的图,而无需在训练过程中使用任何关系数据
DGP可以方便地与神经网络模型相结合,用于下游任务
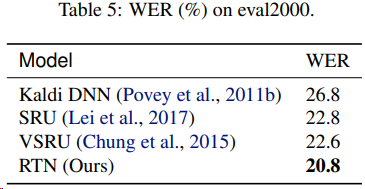
实验结果表明,该方法在语音识别方面优于其他RNN模型
相关资料: